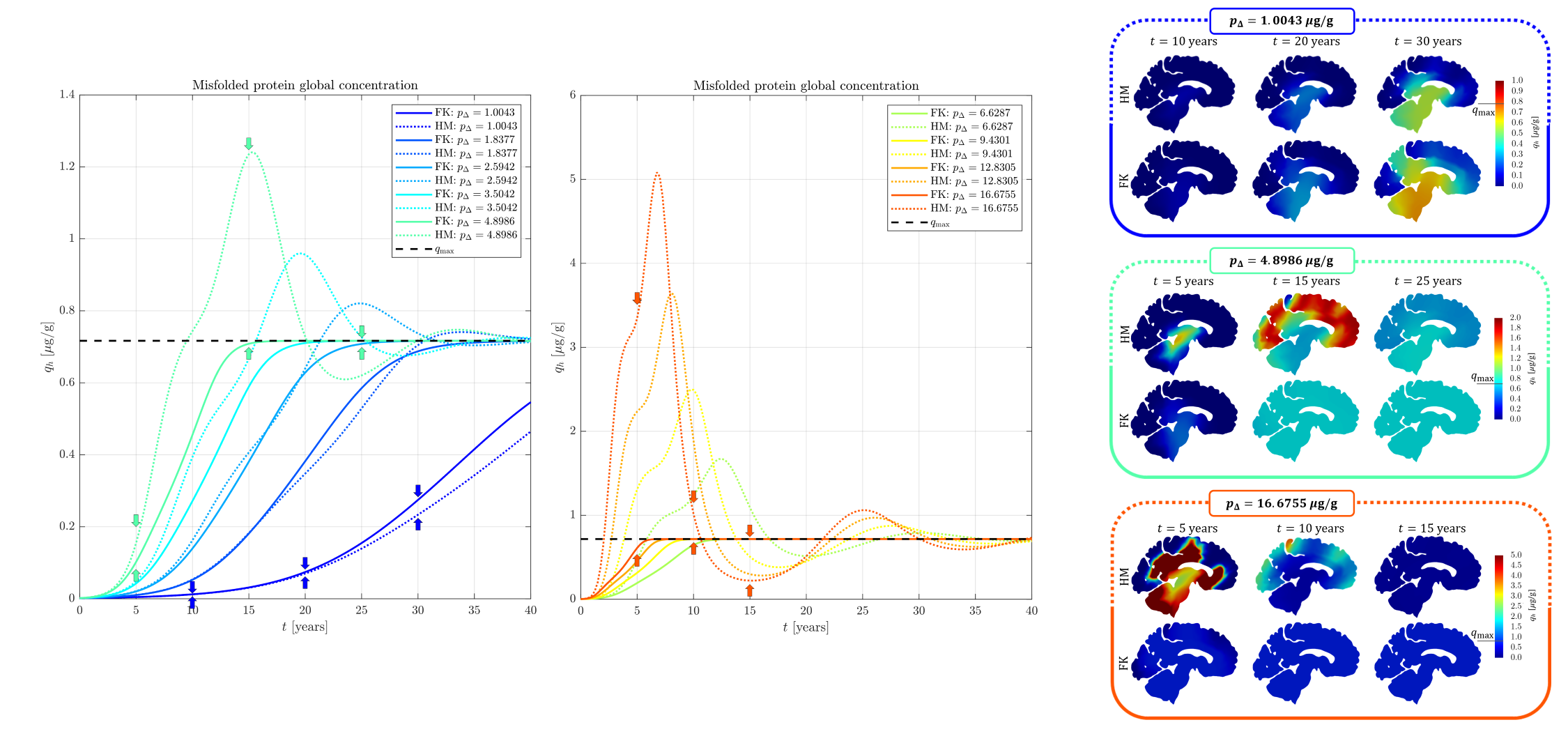
A new MOX Report entitled “Exploring tau protein and amyloid-beta propagation: a sensitivity analysis of mathematical models based on biological data” by Corti, M. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/34-2024.pdf Abstract: Alzheimer’s disease is the most common dementia worldwide. Its pathological development is well known to be connected with the accumulation of two toxic proteins: tau protein and amyloid-beta. Mathematical models and numerical simulations can predict the spreading patterns of misfolded proteins in this context. However, the calibration of the model parameters plays a crucial role in the final solution. In this work, we perform a sensitivity analysis of heterodimer and Fisher-Kolmogorov models to evaluate the impact of the equilibrium values of protein concentration on the solution patterns. We adopt advanced numerical methods such as the IMEX-DG method to accurately describe the propagating fronts in the propagation phenomena in a polygonal mesh of sagittal patient-specific brain geometry derived from magnetic resonance images. We calibrate the model parameters using biological measurements in the brain cortex for the tau protein and the amyloid-! beta in A lzheimer’s patients and controls. Finally, using the sensitivity analysis results, we discuss the applicability of both models in the correct simulation of the spreading of the two proteins.
You may also like
A new MOX Report entitled “Modeling anisotropy and non-stationarity through physics-informed spatial regression” by Tomasetto, M.; Arnone, E.; Sangalli, L.M. has appeared […]
A new MOX Report entitled “Improved amplitude amplification strategies for the quantum simulation of classical transport problems” by Alessandro Andrea Zecchi, Claudio […]
A new MOX Report entitled “Coupled Eikonal problems to model cardiac reentries in Purkinje network and myocardium” by Brunati, S.; Bucelli, M.; […]
A new MOX Report entitled “Variable reduction as a nonlinear preconditioning approach for optimization problems” by Ciaramella, G.; Vanzan, T. has appeared […]