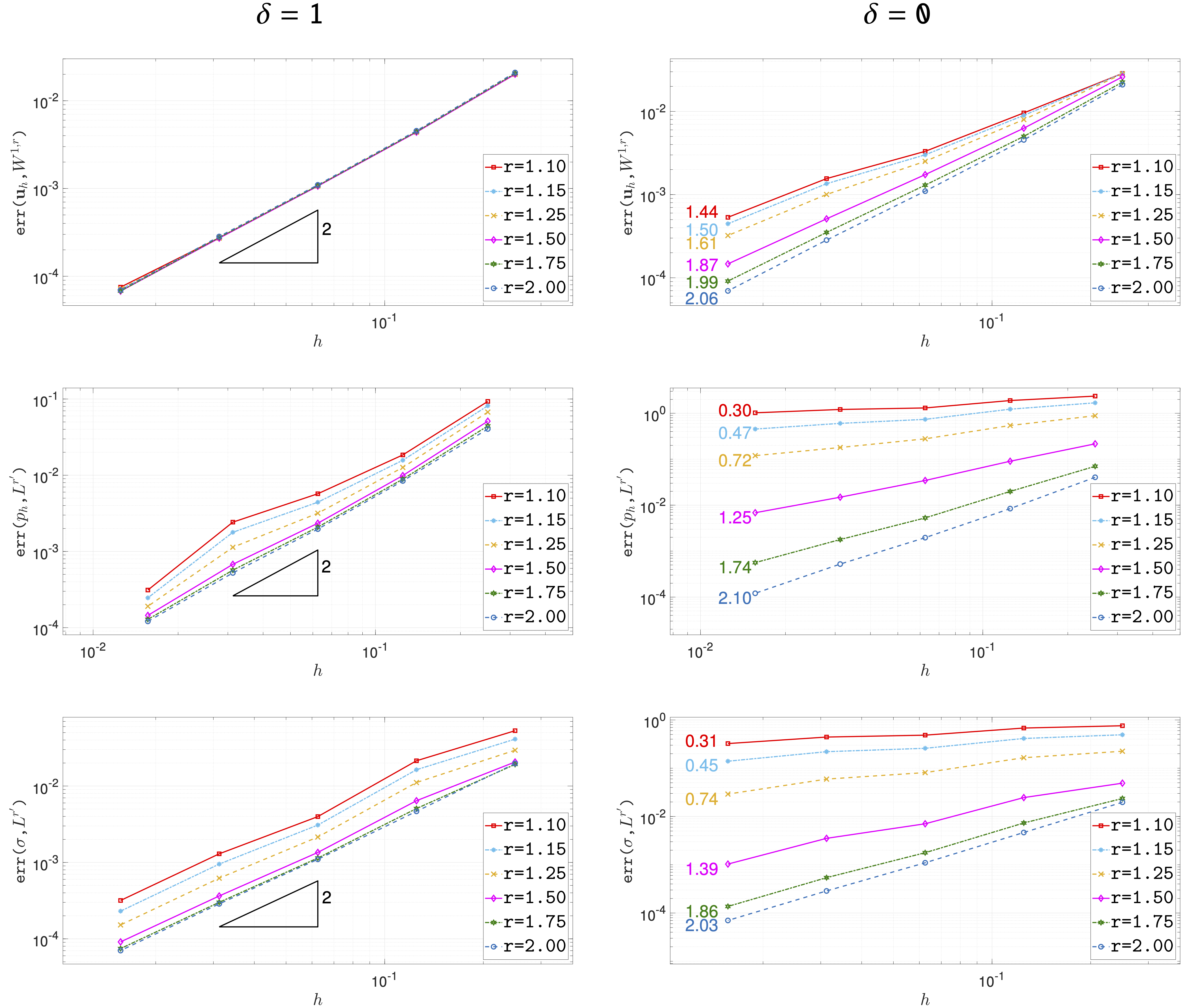
A new MOX Report entitled “A Virtual Element method for non-Newtonian fluid flows” by Antonietti, P.F.; Beirao da Veiga, L.; Botti, M.; Vacca, G.; Verani, M. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/27-2024.pdf Abstract: In this paper, we design and analyze a Virtual Element discretization for the steady motion of non-Newtonian, incompressible fluids. A specific stabilization, tailored to mimic the monotonicity and boundedness properties of the continuous operator, is introduced and theoretically investigated. The proposed method has several appealing features, including the exact enforcement of the divergence free condition and the possibility of making use of fully general polygonal meshes. A complete well-posedness and convergence analysis of the proposed method is presented under mild assumptions on the non-linear laws, encompassing common examples such as the Carreau–Yasuda model. Numerical experiments validating the theoretical bounds as well as demonstrating the practical capabilities of the proposed formulation are presented.
You may also like
A new MOX Report entitled “A fictitious domain formulation based on hierarchical model reduction applied to drug-eluting stents” by Ranno, A.; Ballarin, […]
A new MOX Report entitled “Spatio-Temporal Intensity Estimation for Inhomogeneous Poisson Point Processes on Linear Networks: A Roughness Penalty Method” by Panzeri, […]
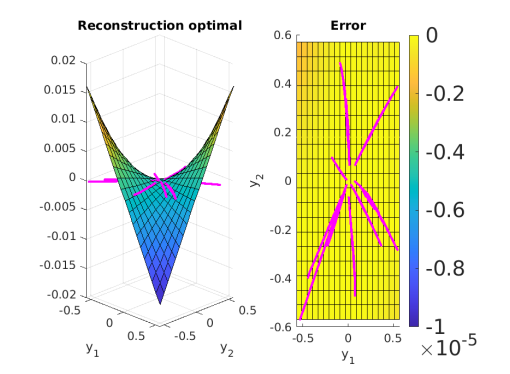
A new MOX Report entitled “Reconstruction of unknown nonlienar operators in semilinear elliptic models using optimal inputs” by Bartsch, J.; Buchwald, S.; […]
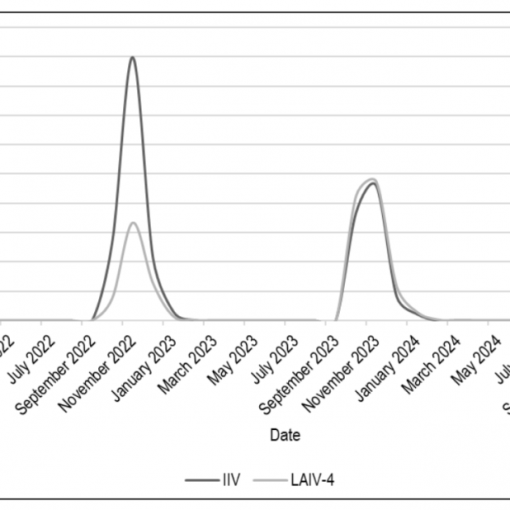
A new MOX Report entitled “Real-World Effectiveness of Influenza Vaccination in Preventing Influenza and Influenza-Like Illness in Children ” by Rigamonti, V.; […]