A new MOX Report entitled “Reconstructing relaxed configurations in elastic bodies: mathematical formulation and numerical methods for cardiac modeling” by Barnafi, N. A.; Regazzoni, F.; Riccobelli, D. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/95-2023.pdf
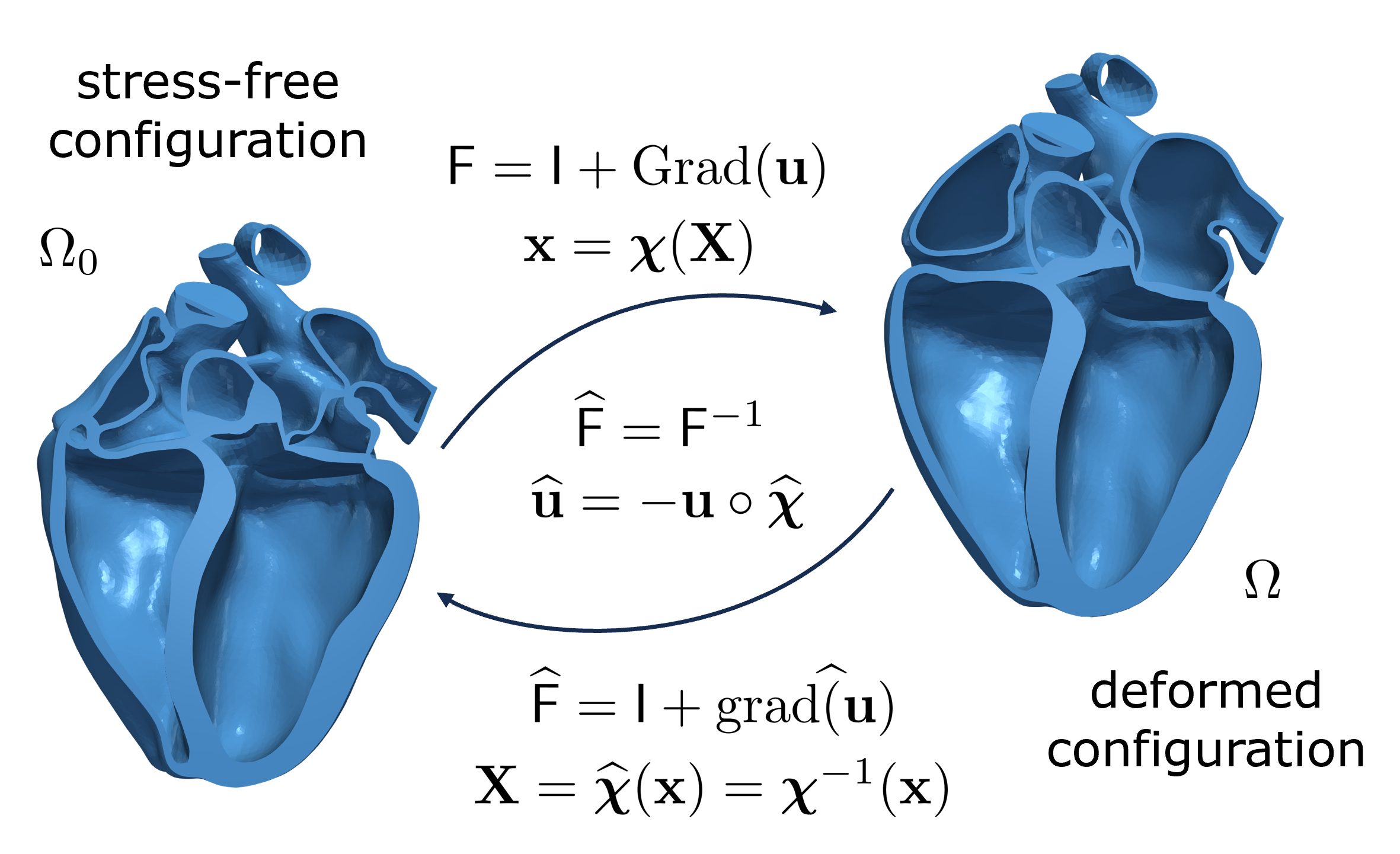
Abstract: Modeling the behavior of biological tissues and organs often necessitates the knowledge of their shape in the absence of external loads. However, when their geometry is acquired in-vivo through imaging techniques, bodies are typically subject to mechanical deformation due to the presence of external forces, and the load-free configuration needs to be reconstructed. This paper addresses this crucial and frequently overlooked topic, known as the inverse elasticity problem (IEP), by delving into both theoretical and numerical aspects, with a particular focus on cardiac mechanics. In this work, we extend Shield’s seminal work to determine the structure of the IEP with arbitrary material inhomogeneities and in the presence of both body and active forces. These aspects are fundamental in computational cardiology, and we show that they may break the variational structure of the inverse problem. In addition, we show that the inverse problem might be il! l-posed, even in the presence of constant Neumann boundary conditions and a polyconvex strain energy functional. We then present the results of extensive numerical tests to validate our theoretical framework, and to characterize the computational challenges associated with a direct numerical approximation of the IEP. Specifically, we show that this framework outperforms existing approaches both in terms of robustness and optimality, such as Sellier’s iterative procedure, even when the latter is improved with acceleration techniques. A notable discovery is that multigrid preconditioners are, in contrast to standard elasticity, not efficient, and domain decomposition methods provide a much more reliable alternative. Finally, we successfully address the IEP for a full-heart geometry, demonstrating that the IEP formulation can compute the stress-free configuration in real-life scenarios where Sellier’s algorithm proves inadequate.