A new MOX Report entitled “Reduced Lagrange multiplier approach for non-matching coupling of mixed-dimensional domains” by Heltai, L.; Zunino, P. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/64-2023.pdf
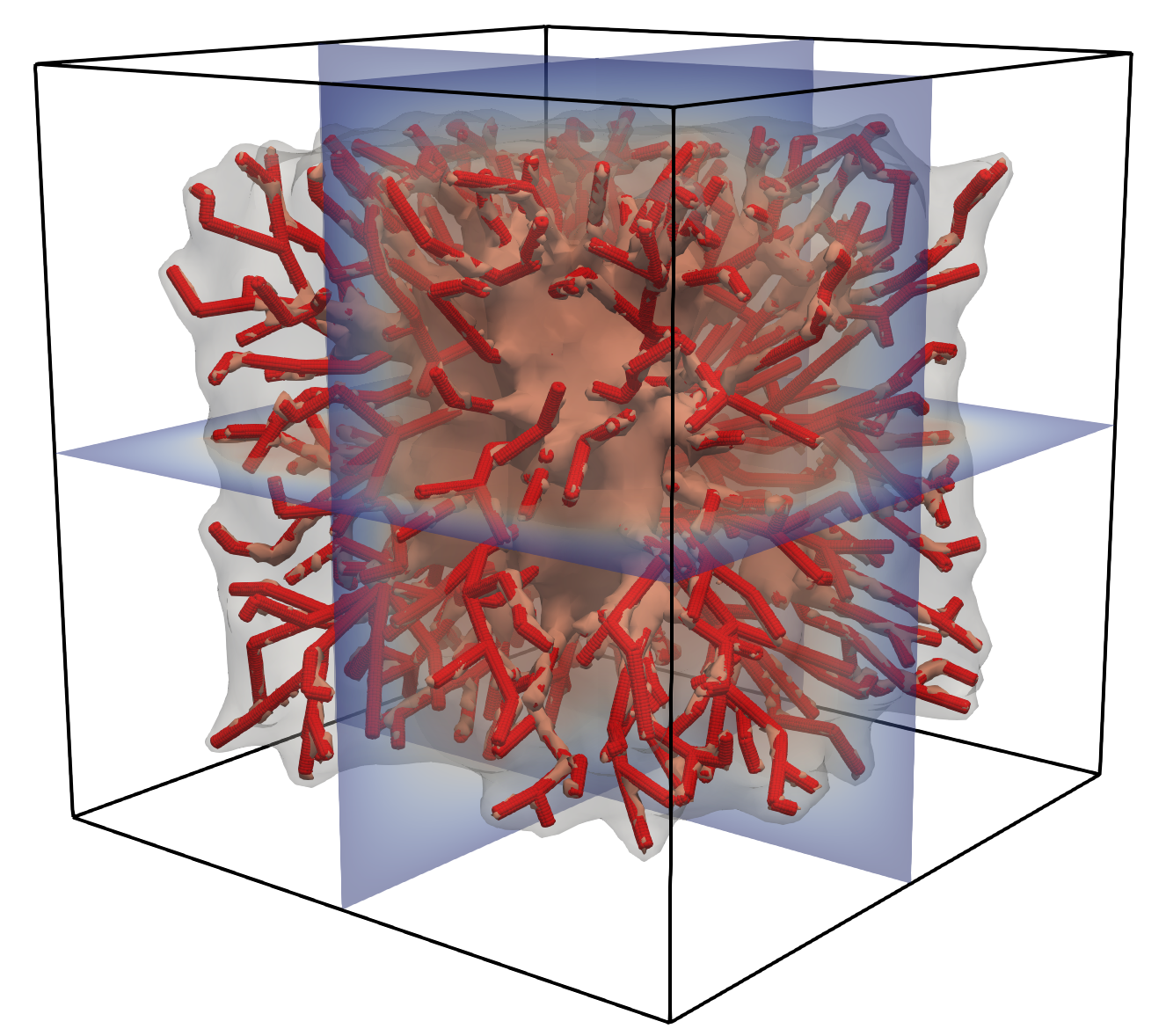
Abstract: Many physical problems involving heterogeneous spatial scales, such as the flow through fractured porous media, the study of fiber-reinforced materials, or the modeling of the small circulation in living tissues — just to mention a few examples — can be described as coupled partial differential equations defined in domains of heterogeneous dimensions that are embedded into each other. This formulation is a consequence of geometric model reduction techniques that transform the original problems defined in complex three-dimensional domains into more tractable ones. The definition and the approximation of coupling operators suitable for this class of problems is still a challenge. We develop a general mathematical framework for the analysis and the approximation of partial differential equations coupled by non-matching constraints across different dimensions, focusing on their enforcement using Lagrange multipliers. In this context, we address i! n abstrac t and general terms the well-posedness, stability, and robustness of the problem with respect to the smallest characteristic length of the embedded domain. We also address the numerical approximation of the problem and we discuss the inf-sup stability of the proposed numerical scheme for some representative configuration of the embedded domain. The main message of this work is twofold: from the standpoint of the theory of mixed-dimensional problems, we provide general and abstract mathematical tools to formulate coupled problems across dimensions. From the practical standpoint of the numerical approximation, we show the interplay between the mesh characteristic size, the dimension of the Lagrange multiplier space, and the size of the inclusion in representative configurations interesting for applications. The latter analysis is complemented with illustrative numerical examples.