On Tuesday 14 February at 2:15 PM in Aula Saleri (VI floor, La Nave Building), Dario Andrini, new MOX postdoc researcher, will deliver a seminar entitled “Optimal design of planar shapes with active materials”.
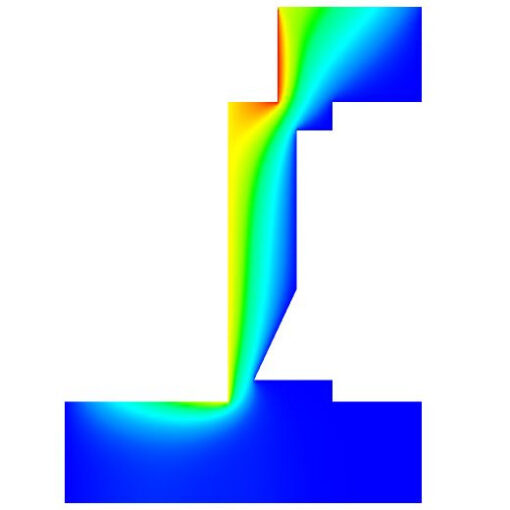
Abstract: Active materials (e.g., polymer gels, liquid crystal elastomers) have emerged as suitable candidates for shape morphing applications, where the configuration of a body is varied in a controlled fashion upon triggering the active response. Given the large variety of these materials, a natural question is to compare different morphing mechanisms for a desired functional shape change and select the most effective one with respect to a certain optimality criterion. To address such a question, we set an optimal control problem that allows to determine the active strains suitable to attain a desired equilibrium transformation, while minimizing the complexity of the activation. Specifically, we discuss the planar morphing of active, hyperelastic bodies in the plain-strain regime, in the absence of external forces.
Our approach aims to be general enough to account for a broad set of active materials through the notion of target metric. For the case of affine shape changes, we derive explicit conditions on the geometry of the reference configuration for the optimality of homogeneous target metrics.
More complex shape changes are then analyzed via numerical simulations. We explore the impact on optimal solutions of different objective functionals, some of them inspired by features of existing active materials. Further, we show how stresses arising from incompatibilities contribute to reduce the complexity of the controls. We believe that our approach may be exploited for the accurate design of active systems and may also contribute to gather insight into the morphing strategies adopted by biological systems, as a result of natural selection.