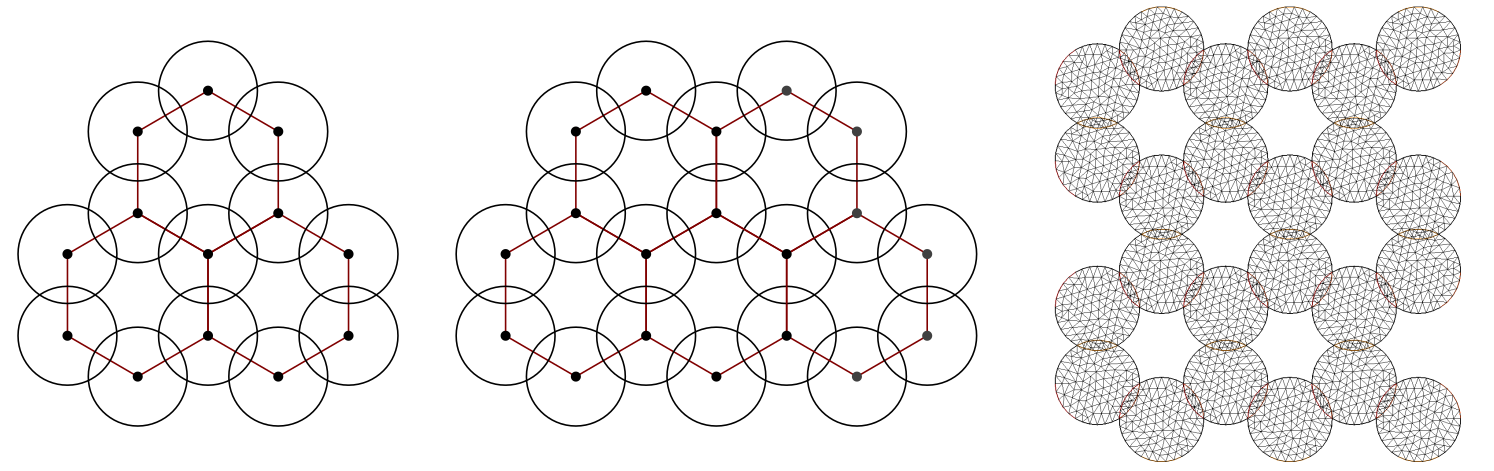
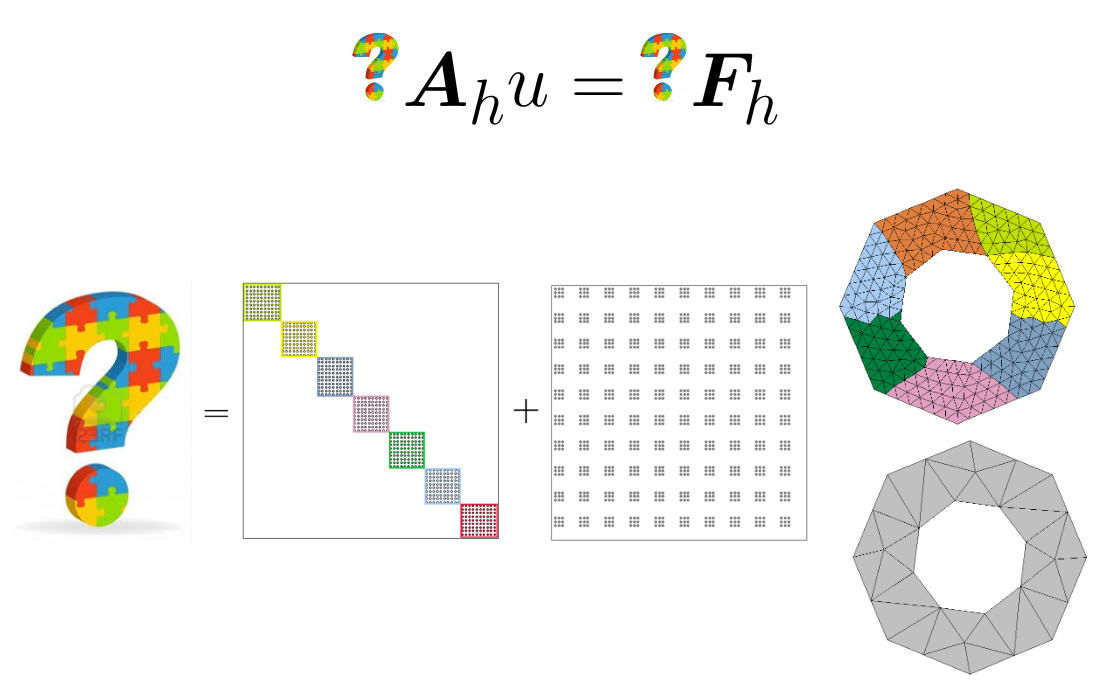
Real-life applications generally require the solution of large-scale algebraic systems arising, for example, from the discretization of partial differential equations. In this context, the fast and accurate solution of large systems of (linear or nonlinear) equations is crucial for enabling new discretization methods. The MOX lab has a long tradition in the development of fast solution techniques either based on parallelizable divide-and-conquer strategies, such as domain decomposition methods, or highly scalable multilevel techniques, such as geometric and algebraic multigrid methods.
- Algebraic methods
- PDE-based methods