A new MOX Report entitled “A high-order discontinuous Galerkin method for the numerical modeling of epileptic seizures” by Leimer Saglio, C. B.: Pagani, S.; Corti, M.; Antonietti, P. F. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/09-2024.pdf
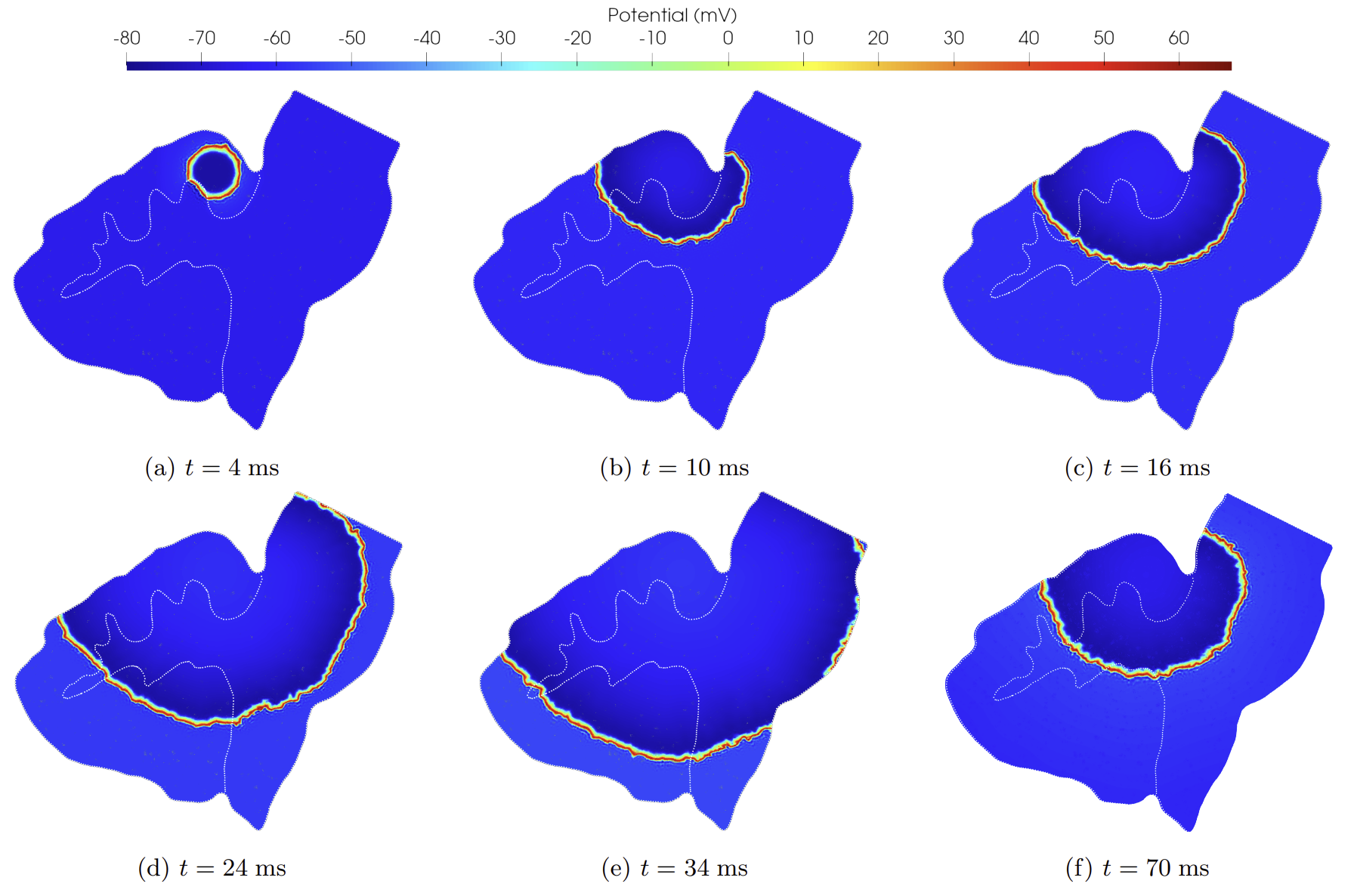
Abstract: Epilepsy is a clinical neurological disorder characterized by recurrent and spontaneous seizures consisting of abnormal high-frequency electrical activity in the brain. In this condition, the transmembrane potential dynamics are characterized by rapid and sharp wavefronts traveling along the heterogeneous and anisotropic conduction pathways of the brain. This work employs the monodomain model, coupled with specific neuronal ionic models characterizing ion concentration dynamics, to mathematically describe brain tissue electrophysiology in grey and white matter at the organ scale. This multiscale model is discretized in space with the high-order discontinuous Galerkin method on polygonal and polyhedral grids (PolyDG) and advanced in time with a Crank-Nicolson scheme. This ensures, on the one hand, efficient and accurate simulations of the high-frequency electrical activity that is responsible for epileptic seizure and, on the other hand, keeps reasonably low the computational costs by a suitable combination of high-order approximations and agglomerated polytopal meshes. We numerically investigate synthetic test cases on a two-dimensional heterogeneous squared domain discretized with a polygonal grid, and on a two-dimensional brainstem in a sagittal plane with an agglomerated polygonal grid that takes full advantage of the flexibility of the PolyDG approximation of the semidiscrete formulation. Finally, we provide a theoretical analysis of stability and an a-priori convergence analysis for a simplified mathematical problem.