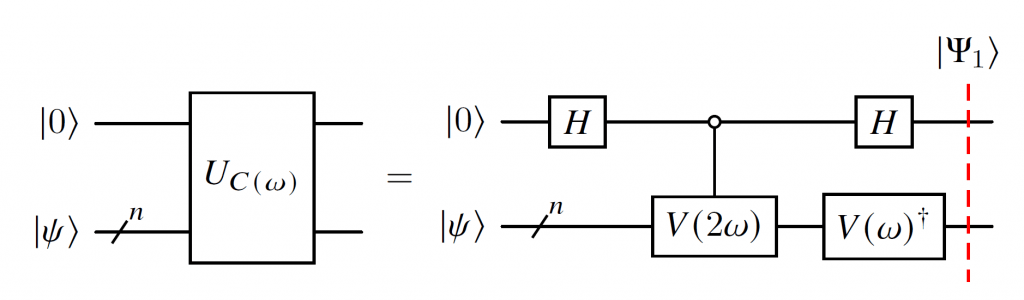A new MOX Report entitled “Block encoding of sparse matrices with a periodic diagonal structure” by Zecchi, A. A.; Sanavio, C.; Cappelli, L.; Perotto, S.; Roggero, A.; Succi, S. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/15-2026.pdf
Abstract: Block encoding is a successful technique used in several powerful quantum algorithms. In this work we provide an explicit quantum circuit for block encoding a sparse matrix with a periodic diagonal structure. The proposed methodology is based on the linear combination of unitaries (LCU) framework and on an efficient unitary operator used to project the complex exponential at a frequency $\omega$ multiplied by the computational basis into its real and imaginary components. We demonstrate a distinct computational advantage with a $\mathcal{O}(\text{poly}(n))$ gate complexity, where $n$ is the number of qubits, in the worst-case scenario used for banded matrices, and $\mathcal{O}(n)$ when dealing with a simple diagonal matrix, compared to the exponential scaling of general-purpose methods for dense matrices. Various applications for the presented methodology are discussed in the context of solving differential problems such as the advection-diffusion-reaction (ADR) dynamics, using quantum algorithms with optimal scaling, e.g., quantum singular value transformation (QSVT). Numerical results are used to validate the analytical formulation.Block encoding is a successful technique used in several powerful quantum algorithms. In this work we provide an explicit quantum circuit for block encoding a sparse matrix with a periodic diagonal structure. The proposed methodology is based on the linear combination of unitaries (LCU) framework and on an effici! ent unita ry operator used to project the complex exponential at a frequency $\omega$ multiplied by the computational basis into its real and imaginary components. We demonstrate a distinct computational advantage with a $\mathcal{O}(\text{poly}(n))$ gate complexity, where $n$ is the number of qubits, in the worst-case scenario used for banded matrices, and $\mathcal{O}(n)$ when dealing with a simple diagonal matrix, compared to the exponential scaling of general-purpose methods for dense matrices. Various applications for the presented methodology are discussed in the context of solving differential problems such as the advection-diffusion-reaction (ADR) dynamics, using quantum algorithms with optimal scaling, e.g., quantum singular value transformation (QSVT). Numerical results are used to validate the analytical formulation.