A new MOX Report entitled “Numerical verification of PolyDG algebraic solvers for the pseudo-stress Stokes problem” by Antonietti, P. F.; Cancrini, A.; Ciaramella, G. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/72-2025.pdf
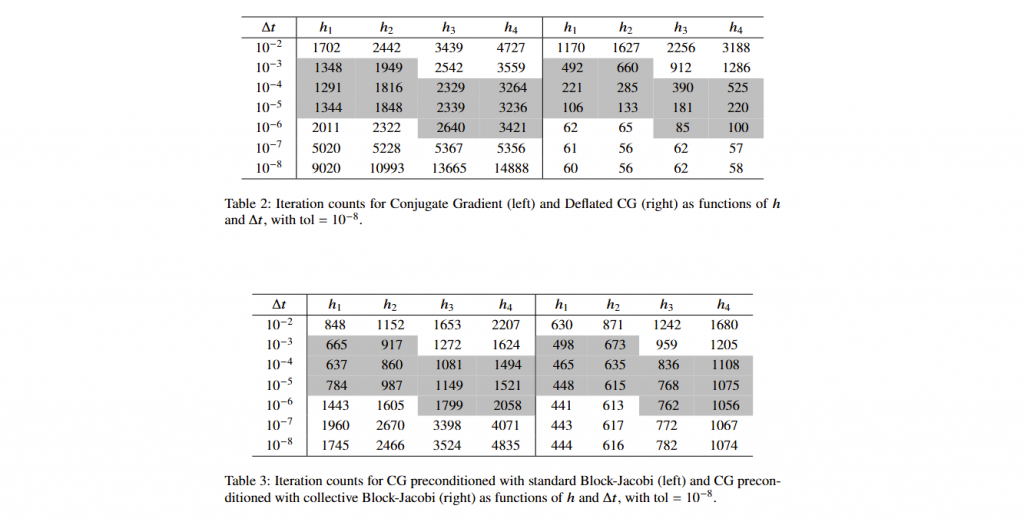
Abstract: This work focuses on the development of efficient solvers for the pseudo-stress formulation of the unsteady Stokes problem, discretised by means of a discontinuous Galerkin method on polytopal grids (PolyDG). The introduction of the pseudo-stress variable is motivated by the growing interest in non-Newtonian flow models and coupled interface problems, where the stress field plays a fundamental role in the physical description. The space-time discretisation of the problem is obtained by combining the PolyDG approach in space with the implicit Euler method for time integration. The resulting linear system, characterised by a symmetric, positive, definite matrix, exhibits deteriorating convergence with standard solvers as the time step decreases. To address this issue, we investigate two tailored strategies: deflated Conjugate Gradient, which mitigates the effect of the most problematic eigenmodes, and collective Block-Jacobi, which exploi! ts the bl ock structure of the system matrix. Numerical experiments show that both approaches yield iteration counts effectively independent of \Delta t, ensuring robust performance with respect to the time step. Future work will focus on extending this robustness to the spatial discretisation parameter h by integrating multigrid strategies with the time-robust solvers developed in this study.