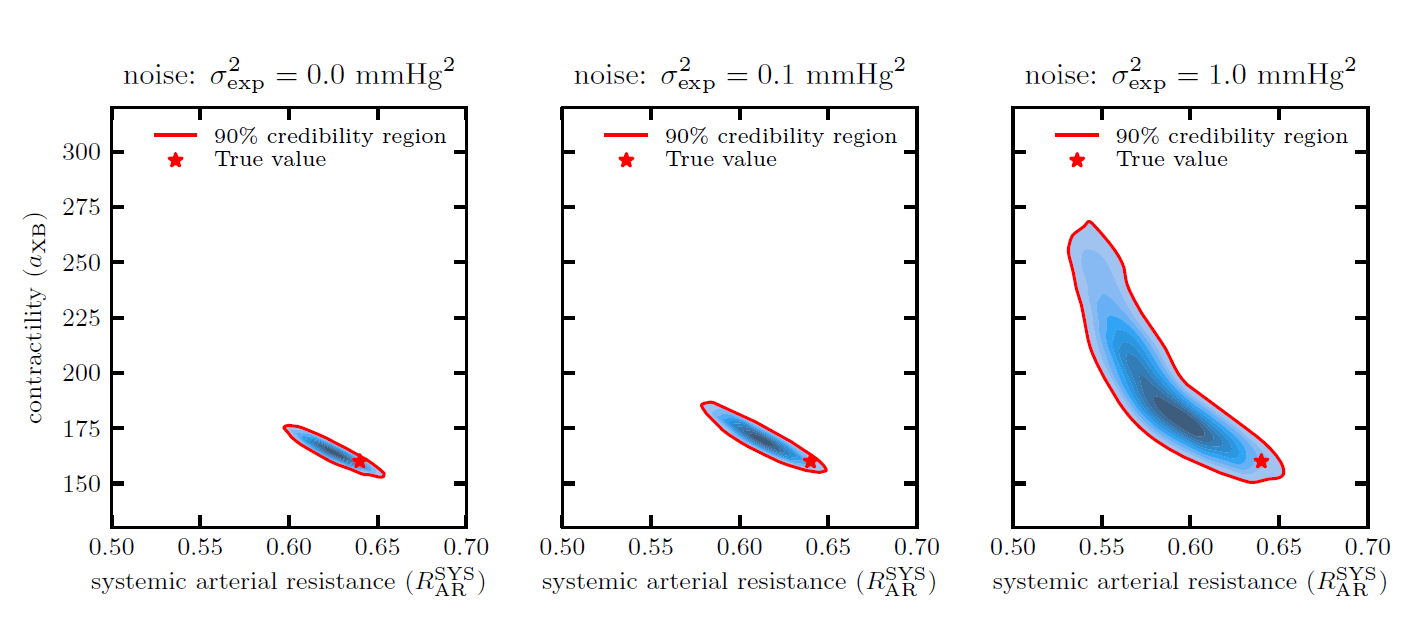
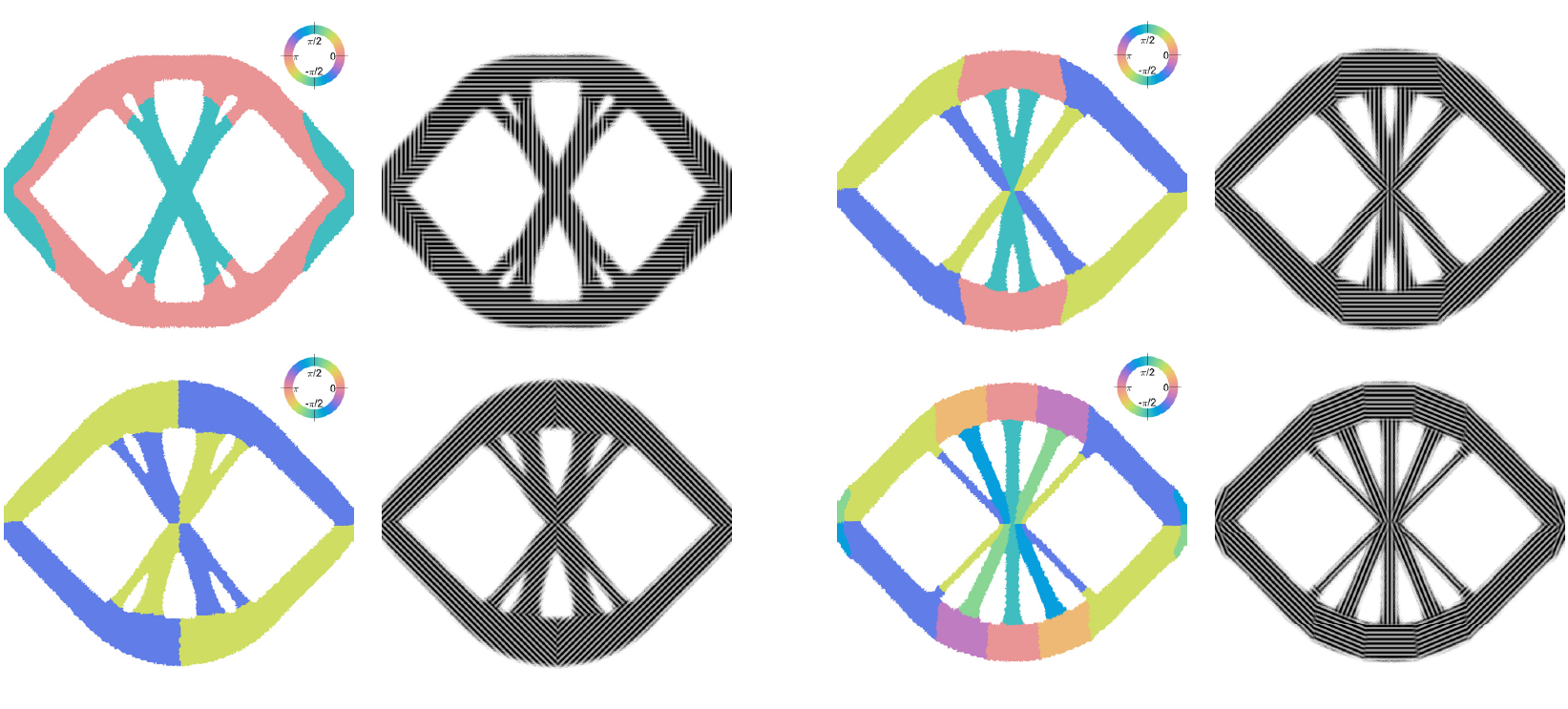
Many problems in Engineering, Life sciences, Natural Sciences, and Finance are modeled as optimization problems, often governed by differential equations. The solution of these problems requires efficient numerical optimization strategies, usually achieved by coupling optimization algorithms with, e.g., appropriate numerical modeling of the governing differential equations and fast solution techniques. This research line addresses shape optimization problems, optimal control problems, inverse problems, and parameter estimation problems and takes full advantage of the synergy between the competencies of the other MOX pillars and actively contributes to their development.
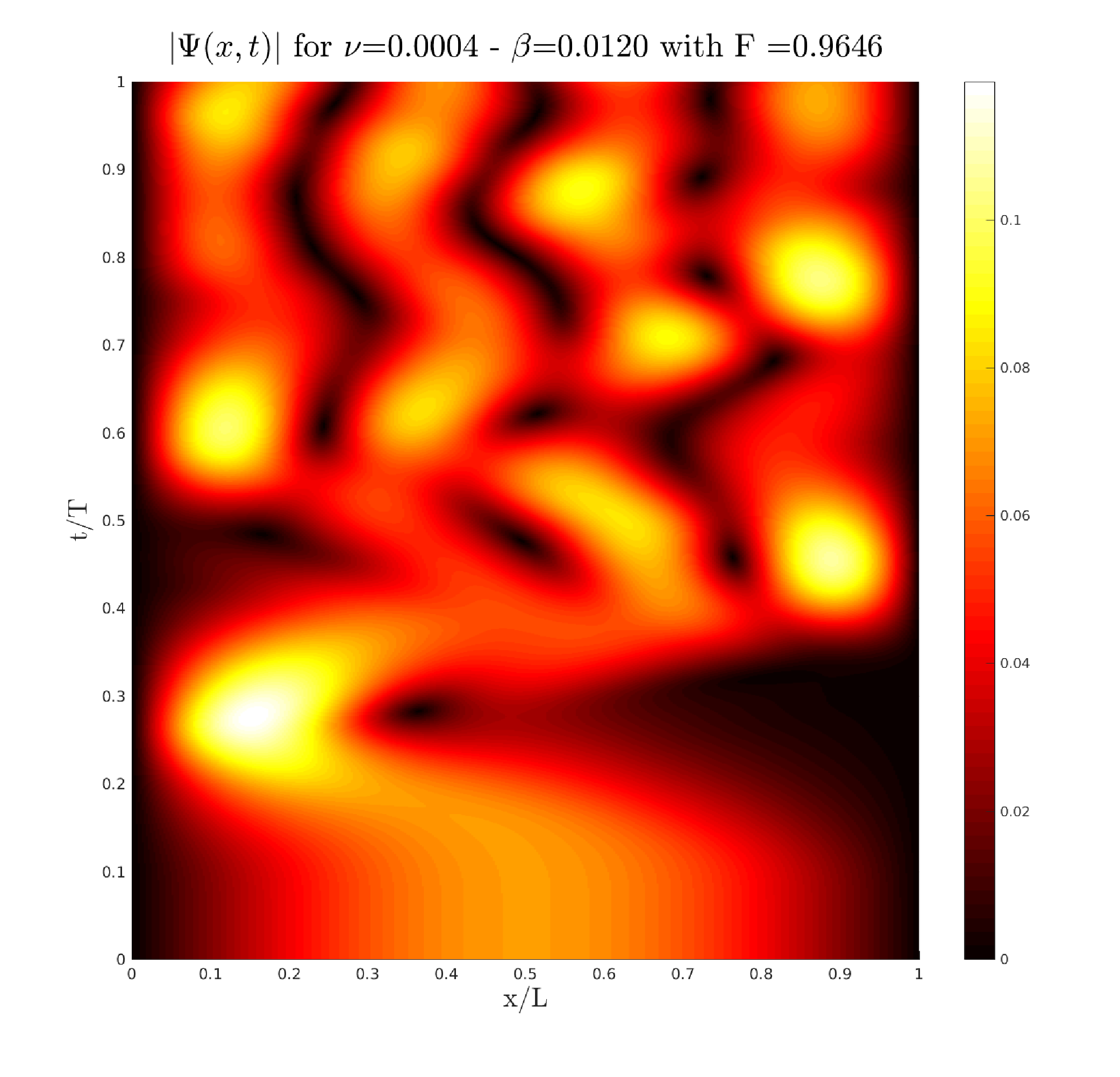
- Inverse problems and parameter estimation
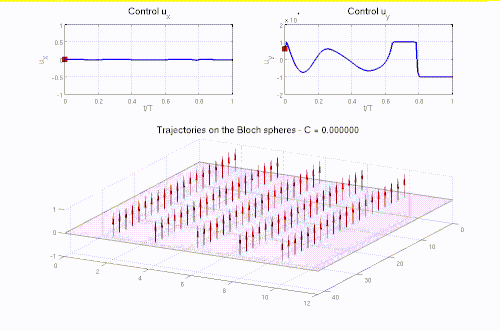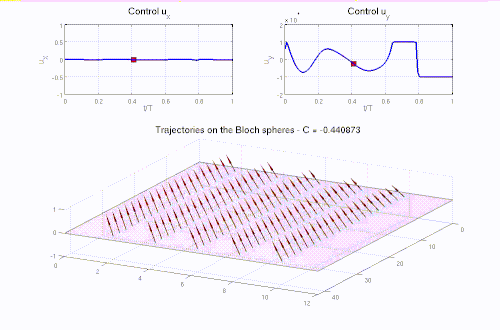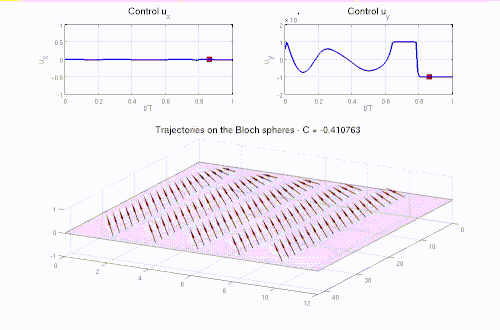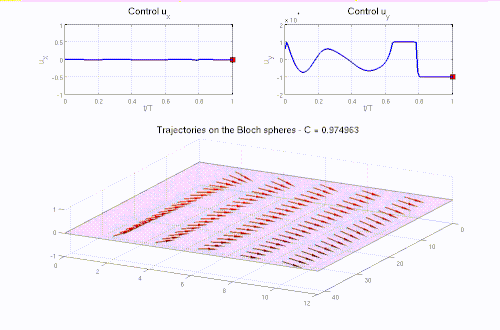
- Optimal control
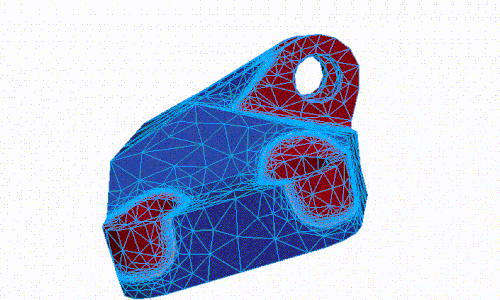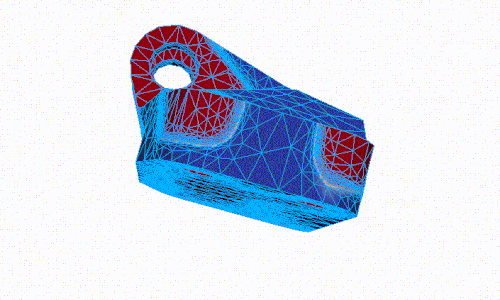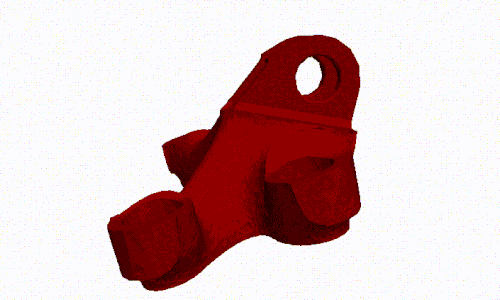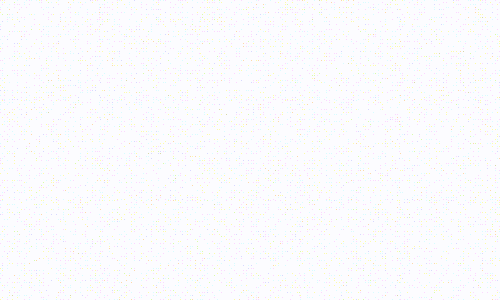
- Shape optimization
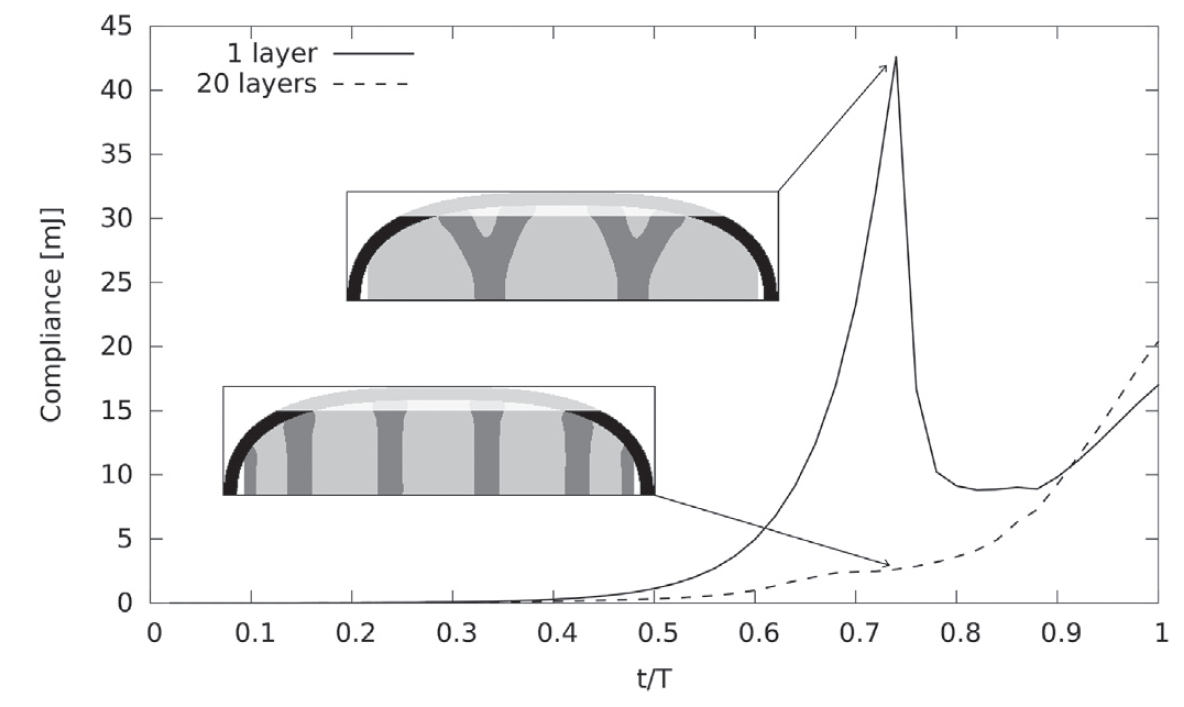
- Topology optimization